Evapotranspiration Data
Methodology
Eddy-Covariance Methodology | Bowen-Ratio Methodology | References
|
Eddy-Covariance Methodology
The eddy covariance energy-budget method (Dyer, 1961; Tanner and Greene, 1989; Bidlake and others, 1996) was used to measure evapotranspiration (ET) for this study.
Eddy covariance instrumentation comprises sonic anemometers and krypton hygrometers that measure latent- and sensible-heat fluxes, respectively. Hygrometer voltage is proportional to attenuated radiation emitted from a hygrometer source tube to a hygrometer detector tube. Voltage fluctuations are related to fluctuations in vapor density by Beer-Lambert Law (Weeks and others, 1987). Sonic anemometers detect changes in the transit time of emitted sound waves to infer fluctuations in wind speed in three orthogonal directions, sonic air temperature, and sensible heat.
Meteorological instrumentation was installed to measure solar radiation, net radiation, soil-heat flux, vapor-density fluctuations, rainfall, soil-moisture content, air and soil temperatures, relative humidity, distance of water above and below land surface, and mean wind speed and direction and the maximum wind gusts measured during a 30-minute averaging period. Minimum and maximum air temperature and relative humidity were identified.
Sites visits were made every month to download data, perform a sensor inspection and other complete equipment maintenance. All instrumentation was visually inspected, leveled, cleaned, or replaced as necessary. Krypton hygrometer source and detector tube windows were cleaned when necessary with a cotton swab and water to remove dust obstructions and restore the signal strength. Net radiometers were releveled, if necessary. Desiccants were replaced to prevent moisture accumulation within instrumentation enclosures. Depth-to-water measurements were taken with a steel or electric water tape from the top of well casings to the water surface. Depth-to-water measurements were used to develop drift corrections for the pressure transducer readings. Digital photographs of the vegetation community were generally taken during monthly site inspections.
For more details on the above methodology, please see the Scientific Investigations Report associated with this data.
Bowen-Ratio Methodology
The Bowen-Ratio method was used to estimate evaporation for site LZ40. Lake evaporation rates (E), in millimeters (mm) per day, were computed as:
![]()
where Qe is the energy used for daily lake evaporation in watts per square meter; λ is the latent heat of vaporization of water as a function of air temperature in joules per kilogram (J kg-1); and ρw is the density of water in kilograms per cubic meter (kg m-3). The Qe is calculated from known components of the daily energy balance for a lake (Eq. 2 in Sumner and Belaineh, 2005; Moreo and Swancar, 2013):
![]()
where Qnr is mean daily net radiation to the lake surface at LZ40; Qas is net energy advected into the lake from lateral flows such as the Kissimmee River; Qag is net energy advected into the lake from groundwater seepage; Qap is energy advected into the lake from precipitation; Qh is sensible heat flux; and Qs is the change in stored heat energy. All terms in Eq. 2 were defined in units of watts per square meter (W/m2). Mean daily values were computed as the average of 96 sub-daily values collected at 15-minute intervals (except 30-minute intervals during period prior to February 7, 2013).
The Qnr was estimated using the CNR1 (Table 1) four-component net radiometer (table 1). The Qas was assumed to be negligible because measured inflows and outflows over a day never exceeded 1 percent of the total lake volume and therefore have little or no effect on the energy budget. Measurements of groundwater seepage were not available to compute Qag. Groundwater seepage was assumed to be zero since lake stage is generally above the surrounding water table so groundwater flow would be from the lake and accurate data to measure this were not available. Advected energy in the control volume through precipitation (Qap) was computed as:
![]()
where Qap is the energy flux associated with a given rainfall volumetric flux qw meters per second (ms-1). Rainfall temperature Ti (°C) over a day is assumed equal to the dew point temperature, computed as a function of air temperature and relative humidity. Rainfall data measured at the LZ40 platform (qw) are provided by the DBHYDRO database. The base temperature (Tb) (Anderson, 1954) was assumed equal to the average water temperature at the LZ40 platform during the study period, as measured by vertical temperature profiles (table 1). Water density (ρw) and specific heat of water (cw) are assumed to have constant values of 1,000 kg m-3 and 4,184 J kg-1 per degree Celsius (°C), respectively.
Sensible heat flux (Qh) is derived from the Bowen (Bowen, 1926) ratio (B) using the following equations:
![]()
with Bowen's ratio equal to:
![]()
where γ is the psychrometric constant in units of kilopascals per degree Celsius (kPa °C-1), computed as a function of atmospheric pressure and air temperature (Fritschen and Gay, 1979); Tws is the average daily temperature of water surface; Ta is average daily air temperature; ew is average daily saturation vapor pressure at the water surface (kPa); and ea is average daily vapor pressure in air (kPa). Vapor pressure was computed as a function of air temperature and relative humidity (Lowe, 1977). Failure of temperature probes that measured the water surface temperature occurred several times during the study period and other sources and methods were utilized. Water surface temperatures from October 7, 2013-February 14, 2014 were obtained from two sources; the SFWMD DBHYDRO data base LZ40 surface water temperature, DBkey IY025 (DBkey is a DBHYDRO assigned unique identifier for a data set), and the following Stefan-Boltzmann Equation:
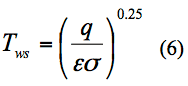
where q is the flux of longwave radiation per unit area out of the water surface from the CNR1 reflected longwave in W/m2, ε is the emissivity of the surface, and δ is the Stefan-Boltzmann constant. The USGS buoy system used to measure surface-water temperature was repaired on February 14, 2014.
The Stefan-Boltzmann Equation was also used to estimate Tws when the surface water temperature buoy system failed on November 3, 2015 due to wave action and was repaired 16 December 2015. In late 2015, the lake Bottom + 2 ft, + 8 ft, and + 14 ft water temperature probes were reading higher than the other water temperature probes. The error had slowly increased since March 30, 2015 and all water temperature probes were replaced on 16 December 2015. The problem persisted and the Campbell Scientific AM 16/32 Channel Relay Multiplexor was replaced April 28, 2016, but this did not resolve the problem. The water temperature data for the affected probes was estimated as the average of water temperatures of the probes adjacent to the affected probe.
Changes in heat energy stored within the control volume (Qs) for a given day are given by:
![]()
where D was the depth of the lake in feet, ![]() and
and ![]() are depth-wise integrated lake water temperatures measured at the beginning (i-1) and end (i) of a day, respectively. Integrated water temperatures (
are depth-wise integrated lake water temperatures measured at the beginning (i-1) and end (i) of a day, respectively. Integrated water temperatures (![]() ,
, ![]() ) were computed using a backward (1-day) moving average of submerged thermistors (table 1) to minimize spurious values created by local thermal eddies in the vicinity of the LZ40 platform. Combining eqns. 1 and 3-7, the equation for calculating daily evaporation as (E) (Moreo and Swancar, 2013) is given as:
) were computed using a backward (1-day) moving average of submerged thermistors (table 1) to minimize spurious values created by local thermal eddies in the vicinity of the LZ40 platform. Combining eqns. 1 and 3-7, the equation for calculating daily evaporation as (E) (Moreo and Swancar, 2013) is given as:
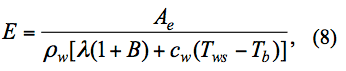
![]()
where Ae is available energy. Unrealistically large evaporation rates occurred when daily Bowen ratios were between -0.65 and -1.3 (German, 2000). These unrealistic values (occurring in 4 percent of the evaporation dataset) were removed and replaced by assuming complete conversion of net radiation to evaporation. Negative values for E were set to zero since negative values are something other than evaporation and may represent dew formation or fog.
References
Anderson, E.R., 1954, Energy-budget studies, in Water-loss investigations: Lake Hefner studies, technical report: U.S. Geological Survey Professional Paper 269, p. 71-119, http://pubs.er.usgs.gov/publication/pp269.
Bidlake, W.R., Woodham, W.M., and Lopez, M.A., 1996, Evapotranspiration from areas of native vegetation in west-central Florida: U.S. Geological Survey Water-Supply Paper 2430, 35 p.
Bowen, I. S., 1926, The ratio of heat losses by conduction and evaporation from any water surface, Physics Review, v. 27, p. 779-787.
Dyer, A.J.: Measurements of evaporation and heat transfer in the lower atmosphere by an automatic eddy covariance technique: Quarterly Journal of the Royal Meteorological Society, v. 87, p. 401-412, 1961.
Fritschen, L. J. and Gay, L. W., 1979, Environmental Instrumentation, Springer-Verlag, New York, 209 pp.
German, E.R., 2000, Regional Evaluation of Evapotranspiration in the Everglades: U.S. Geological Survey Water-Resources Investigations Report 00-4217, 48 p.
Lowe, P.R., 1977, An approximating polynomial for the computation of saturation vapor pressure: Journal of Applied Meteorology, v. 16, no. 1, p. 100-103. http://dx.doi.org/10.1175/1520-0450(1977)016<0100:AAPFTC>2.0.CO;2.
Moreo, M.T. and Swancar, A., 2013, Evaporation from Lake Mead, Nevada and Arizona, March 2010 through February 2012: U.S. Geological Survey Scientific Investigations Report 2013-5229, 40 p., http://dx.doi.org/10.3133/sir20135229.
Shih, S.F., 1980, Water budget computation for a shallow lake - Lake Okeechobee, Florida: Water Resources Bulletin, JAWRA Journal of the American Water Resources Association, 16: 724-727. doi: http://dx.doi.org/10.1111/j.1752-1688.1980.tb02455.x.
Sumner, D.M. and Belaineh, G., 2005, Evaporation, Precipitation, and Associated Salinity Changes at a Humid, Subtropical Estuary: Estuaries, v. 28, no. 6, p. 844-855.
Tanner, B.D., and Greene, J.P., 1989, Measurement of sensible heat and water vapor fluxes using eddy covariance methods: Final report prepared for U.S. Army Dugway Proving Grounds, Dugway, Utah, 17 p.
Weeks, E.P., Weaver, H.L., Campbell, G.S., and Tanner, B.D., 1987, Water use by saltcedar and by replacement vegetation in the Pecos River floodplain between Acme and Artesia, New Mexico: U.S. Geological Survey Professional Paper 491-G, 37 p.